Teoria
Zagadnienia matematyczne związane z wyprowadzeniem algorytmu, na którym opiera się AKS, są dosyć proste.
Wiadomo bowiem, że dla n liczb pierwszych zachodzi następujące równanie:
a dla jednego, wyszczególnionego wielomianu w(x)=x-a uogólnienie równa się:
 P.
Jest to w pewnym sensie test pierwszości, jednak jeszcze nie taki jak jest potrzebny.
To równanie ma złożoność wykładniczą i nie nadaje się do dużych liczb, jednak po zastosowaniu specjalnego wielomianu
P.
Jest to w pewnym sensie test pierwszości, jednak jeszcze nie taki jak jest potrzebny.
To równanie ma złożoność wykładniczą i nie nadaje się do dużych liczb, jednak po zastosowaniu specjalnego wielomianu AKS ma dwie części dążące do sprawdzenia, czy liczba n jest potęgą liczby pierwszej. Pierwsza to znalezienie parametrów równania r i s. W drugiej fazie algorytmu sprawdzane są wartości b względem s.
Istnieją dwa twierdzenia AKS i AKS z rozwinięciem Lanstra.
Pierwsze z nich jest nieco gorsze i w dalszej części tworzenia algorytmu AKS trzeba korzystać z twierdzenia Fouvryego, przez co stosowane jest twierdzenie drugie.
Należy założyć, że n∈C+ i tak jak r jest liczbą pierwszą, a v rzędem n modulo r.
Dalej zbiór S jest zbiorem s liczb a i a’ całkowitych,
takich że ich NWD wynosi 1, a dla każdego d, które jest dzielnikiem φ(r)/ν zachodzi nierówność:
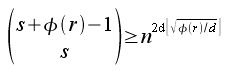
oraz dla wszystkich a S w pierścieniu Zn[x]/xr-1 zachodzi równanie
S w pierścieniu Zn[x]/xr-1 zachodzi równanie
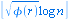 Jeśli dla wszystkich a równanie pozostaje spełnione, to wiadomo, że n jest liczbą pierwszą.
Jeśli dla wszystkich a równanie pozostaje spełnione, to wiadomo, że n jest liczbą pierwszą.
Opis algorytmu
Jest wiele rozwinięć algorytmów AKS. Wszystkie oczywiście opierają się na podstawowym, jednak są modyfikacje przyśpieszające działanie. Zmiany i ulepszenia do AKS wprowadzali rożni naukowcy, profesorowie, jednak najlepsze i najważniejsze zmiany wprowadzili Lenstra i Bernstein. Właśnie metoda Lenstry odniosła największy sukces. Warto więc skupić się na opisie algorytmu testu liczb pierwszych z zastosowaniem zmian, udogodnień wprowadzonych przez Hendrika Lenstra.
Ogólnie można przyjąć, że implementację tego algorytmu można zapisać jako pięciokrokowy plan, w którym poszczególne kroki to dążenie do pewności pierwszości podanej liczby. Na początku trzeba sprawdzić czy liczba, która ma zostać przetestowana jest większa od 1. Jest to zupełnie normalne, gdyż liczba 1, nie jest liczbą pierwszą i nie potrzebne są dalsze obliczenia. Należy więc brać do testowania liczby większe od jeden. Symbolicznie liczbę testowaną można przyjąć jako n. Za n więc będą podstawiane dowolne liczby, które algorytm ma sprawdzić i ustalić ich pierwszość.
Krok pierwszy to sprawdzenie czy:
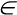 N i b>1
N i b>1Krok drugi, czyli znajdowanie liczby r, liczby potrzebnej w głównym teście AKS. W kroku tym nie zachodzi sprawdzanie liczby n, a jedynie wyznaczanie liczby potrzebnej do późniejszych obliczeń. Najmniejszą liczbę r szuka się ze wzoru:
Krok trzeci to wyliczanie podwójnej nierówności:
Krok czwarty to bardzo łatwy test. Polega jedynie na sprawdzeniu, czy liczba n jest mniejsza, bądź równa r. Jeżeli warunek jest spełniony, podana liczba testowa, jest liczbą pierwszą i nie trzeba przechodzić do ostatniego testu AKS.
Krok piąty - AKS!
Dla liczby a z przedziału od 1 do pierścienia 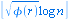 sprawdzana jest nierówność.
φ(r) to funkcja Eulera określająca ilość liczb względnie pierwszych z liczbą r.
Równanie AKS sprawdzania pierwszości liczby n wygląda następująco:
sprawdzana jest nierówność.
φ(r) to funkcja Eulera określająca ilość liczb względnie pierwszych z liczbą r.
Równanie AKS sprawdzania pierwszości liczby n wygląda następująco:
Są liczby, zwane liczbami Carmichaela, które nie spełniają założenia i przechodzą przez test AKS. Są to np. liczby:
| 561 | = | 3 · 11 · 17 | Najmniejsza z tych liczb |
| 1105 | = | 5 · 13 · 17 | (4 | 1104, 12 | 1104, 16 | 1104) |
| 1729 | = | 7 · 13 · 19 | (6 | 1728, 12 | 1728, 18 | 1728) |
| 2465 | = | 5 · 17 · 29 | (4 | 2464, 16 | 2464, 28 | 2464) |
| 2821 | = | 7 · 13 · 31 | (6 | 2820, 12 | 2820, 30 | 2820) |
| 6601 | = | 7 · 23 · 41 | (6 | 6600, 22 | 6600, 40 | 6600) |
| 8911 | = | 7 · 19 · 67 | (6 | 8910, 18 | 8910, 66 | 8910) |
Przechodzą one sam test AKS, jednak nie przechodzą pozostałych, wiec cały test jest deterministyczny dla wszystkich liczb naturalnych.